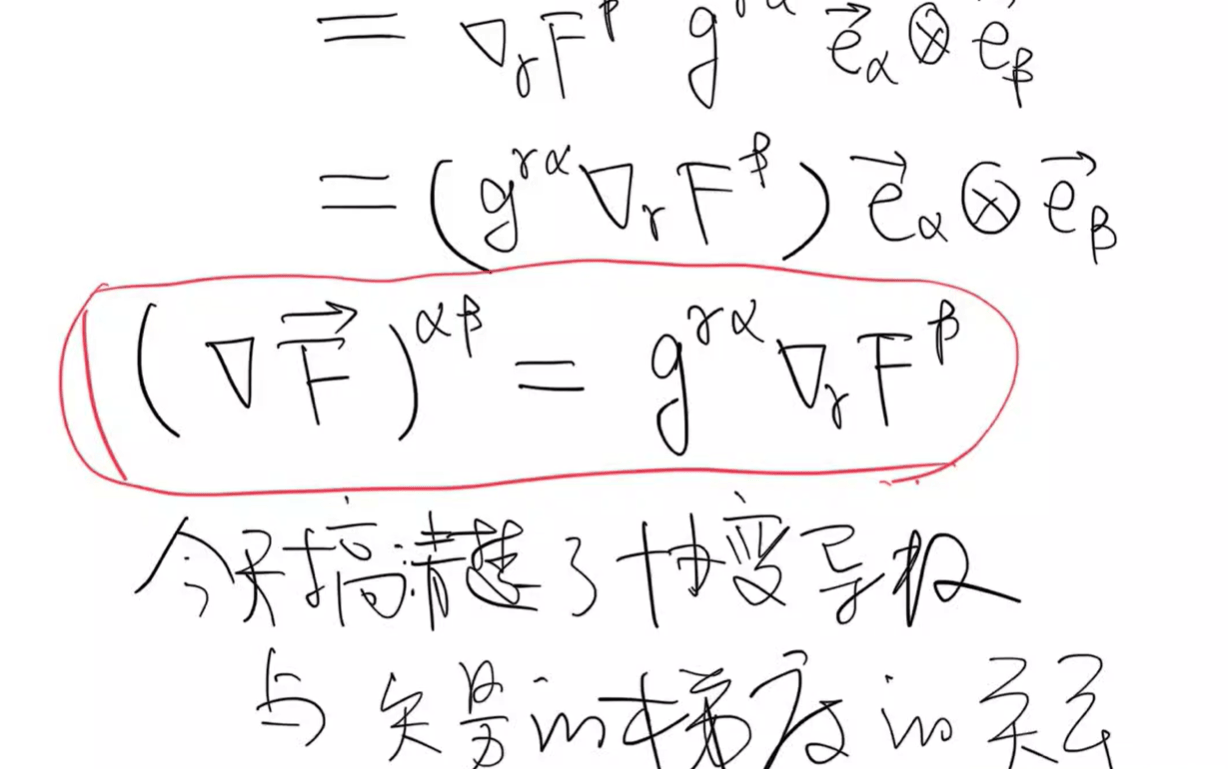
如何从矢量演算变成差异几何变化?男高音的梯度是什么? 5月4日12:00,启动了“张乔阳班级”的245阶段。 Sohu的创始人,董事长兼首席执行官兼物理博士Zhang Chaoyang在Sohu Video Live Broadcast Room中。他首先检查了如何用载体的二元基础语言表达差异的原理,并评估了向上和较低的矢量,男高音和指标的相关含义。接下来,他以向量的双基础语言引入了零级张量(标量)的梯度,本质上是一个一阶男高音,可用于简化任何次要删除下标量场变化的体积的计算。后来,他还比较了这一含义,将梯度引入了一阶张量(向量),并将其与协变量衍生物进行了比较。由向量,力学,电动力学,亲戚,身体定律甚至许多物理量不会改变坐标系统的选择或变化。例如,由于洛伦兹的变化,轻速不会改变。在三维空间中,无论旋转如何,向量的长度保持不变。要了解不变性,通常有必要使用矢量计算工具来描述这些数量或法律。在更一般的情况下,在四维弯曲的时空和一般亲戚相关的空间中对物理定律的研究需要使用更通用的矢量计算,即多样性的几何形状。为什么称为“自定义”几何形状? Pinalzhang Chaoyang说,从差异的角度来看,在几何形状的差异中,人们在歧视中研究了几何特性,并且从其差异的角度来看,从其差异的角度来看,如果时间和空间本身是直的或弯曲的,则可以描述改变空间和空间坐标的物理体积的性质。改变物理带有时空坐标的ICAL数量对应于空间时间坐标的提取的坐标,换句话说是差异。在几何形状的差异中,男高音是重要的事情。当更改坐标系时,张量组件可能会更改,但是张量不会改变。在一般书籍中,经常通过确定在坐标系转换下转换相应的男高音组件的规则来解释男高音的不变性。在PAG研究期间,Zhang Chaoyang发现,与数学的抽象定义相比,基于计算欧几里得空间中向量的经验,使用向量的双基础来理解差异几何变化不仅易于理解,而且在表达计算中也更短。在这类物理学中,他将带领网民审查此方法,然后回答零级张量(标量)和FIR之间的变化的问题T级张量(向量)。这种类型的问题通常在流体机械师等领域遇到,并且我们已经在以前的物理学中与该主题有一些初步联系。张·乔阳首先引入了张量的符号和定义,这与矢量微积分相似,而男高音可以表示为扩展elextextext
他们分别为零,一阶,二阶和三阶男高音。该表示与坐标系无直接相关,这也意味着这些数量不会改变坐标系。选择坐标系后,将获得上下向量,并相应地获得
他们喜欢点产品的关系
一阶张量可以表示为
指数中的f^α称为相反物质。相同的一阶张量也可以表示为
指标在表面的F_α下方是协变量的组件。同样,使用鞋面的不同组合较低的基础向量,二阶男高音可以以不同的形式写入。
张·乔阳提醒人们,上面编写公式的技巧是确保满足爱因斯坦的规则。从这里开始,我们获得了二阶男高音的不同部分,他们的索引写作方法也有所不同。在某些情况下,在上面的公式中描述的,从上到下,(2,0)的物质(或相反物质),(0,2)的物质类型(或协变量成分)和(1,1)张量张量张量张量张量t均受到尊重。对于高阶张量,可以进行类似的讨论和评论。
在介绍了张量的符号和定义之后,我们需要注意特殊的第一阶张量 - 协调惯常的男高音,定义为:
在力学中,它描述了颗粒的小运动,也可以称为切线向量。通过使用点复制,您可以找到坐标的自定义坐标器的长度:
更一般地,可以表示为:
此步骤是指尺度,这是两个基本向量的点的再现
量表的相反也可以通过上层载体的点再现相似地定义
比例尺,反之亦然,能够提起和减少指标。首先,让我们研究如何使用指标来实现基本向量的升力和降低。请注意,基本向量本身也是向量,当量表在基本向量上作用时,
模拟(1),最后一个边缘的均等签名可能被认为是在一组较低的基础向量中扩展的E^β,因此应该有
也就是说,标准将下部基箭头提升到上底箭头。接下来,评估了成分的测量和降低的效果。对于逆变器,有
知道量表可以提高基本向量,因此应该有
也就是说,刻度将逆变器的一部分减少到协变量物质。规模是上层矢量和下基矢量之间的一对一字母。因此,可以认为上层矢量和下基矢量描述了相同的矢量空间,但是选择了两组不同的基本矢量集来研究此空间。
(Zhang Chaoyang介绍了如何使用尺寸指数提升)
零级张量的梯度(标量)
在向量的双重基础的框架中,可以研究不同男高音的梯度的定义。梯度是改变男高音的成本。在三维笔直空间的矩形坐标系中,最多的是零级张量(标量)的总变化。根据多元函数的泰勒的扩展,可以将其写入每个方向的独立变化之和。
同时,在同一坐标系下,坐标的微小变化可以表示为向量
我,j和k是卡特斯中向量的三个方向伊恩坐标。以这种方式,可以以两个向量点的形式重新编写上述变化:
指定向量
这里指定的向量F非常有用。例如,当在去除坐标的某些方向上找到由标量字段引起的变量数时,坐标拆卸方向可能会有所不同,但是找到相应的变量数不需要独立的计算。从上面的派生中,我们可以看到,仅通过了解向量F并通过特定的坐标去除矢量f来产生它,我们就可以得到相应的变化量。张·乔阳(Zhang Chaoyang)介绍了以这种方式指定的向量是梯度,并且不取决于它。对于更改的特定方向,它将是高于原始体积的订单。例如,零阶张量(标量)的梯度这是一阶张量(向量)。
以上仅专注于特殊情况。可以为通用坐标系完成此操作吗? a g零级张量(标量)场是每个坐标的函数。随着泰勒的扩张,一阶男高音可以写为
根据直觉,可以写下以下方程式:
因此,该向量f可以作为
提供了该梯度向量的协变量和相反的组成部分,即扩展下部基矢量和上层载体的系数。同时,可以看出,标量梯度的相对部分可以通过公制升高指数从协变量获得
总之,本节讨论了零级张量梯度的定义。标量的微观变化可以写入不取决于坐标数的微量器和坐标数字微量器的矢量的繁殖点。该向量是梯度,张量遵循的量增加了从标量到向量的顺序。
(张乔阳具有零级t的梯度含义恩索)
一阶张量的梯度(向量)
对于一阶张量(矢量)场,它还可以贝拉兰(Beralan)的变化是由微弹药坐标引起的。类似于零量张量(标量),我们可以定义一阶张量(向量)的梯度,从而简化了发现一阶张量(矢量)更改的问题吗?一阶张量(矢量)的更改是否可以写为二阶张量和坐标微元素?在这个现场班级中,张乔阳还向网民回答了这两个问题。
根据上一节中的想法,有望引入二阶张量t,以表达一阶张量F的变化df的值为
在最后一步中,t扩大(1,1)组件,目的是促进下一次冷凝。继续计算,您可以得到
在括号中是变量值的相对部分
同时,Zhang Chaoyang概括的现场课程解释说樟宜NG应使用协变量衍生物计算一阶张量。这是因为与标量不同,每个张量组件的含义取决于基本向量,它们的更改包括由向量转换引起的组件,这需要仔细处理。使用协变量,
在
γ是与指标兼容的相互作用。将此结果与等式(2)进行比较,可以找到
也就是说,一阶张量的相对部分的协变量是该一阶张量的梯度(二阶张量)的(1,1)部分。
简而言之,一阶张量(矢量)的梯度是二阶张量
物质和基本矢量被指标升高和降低,并且可能会重写:有:
因此,显然我们知道协变量衍生物与矢量梯度之间的关系,实际上它们是同一件事。
(张·乔阳(Zhang Chaoyang)分享了协变量和V之间的关系椭圆梯度)
据了解,周日中午12点在SOHU视频中现场直播“张乔阳班”。网民可以搜索“ Zhang Chaoyang”来“遵循SOHU视频应用程序的流”,以观看实时广播和过去的完整视频重播;关注“张” Chaoyang的物理课程“当然要查看“知识点”的简短视频;此外,您还可以在SOHU新闻应用程序的“ Sohu Technology”帐户上查看每个物理课程的详细文章。
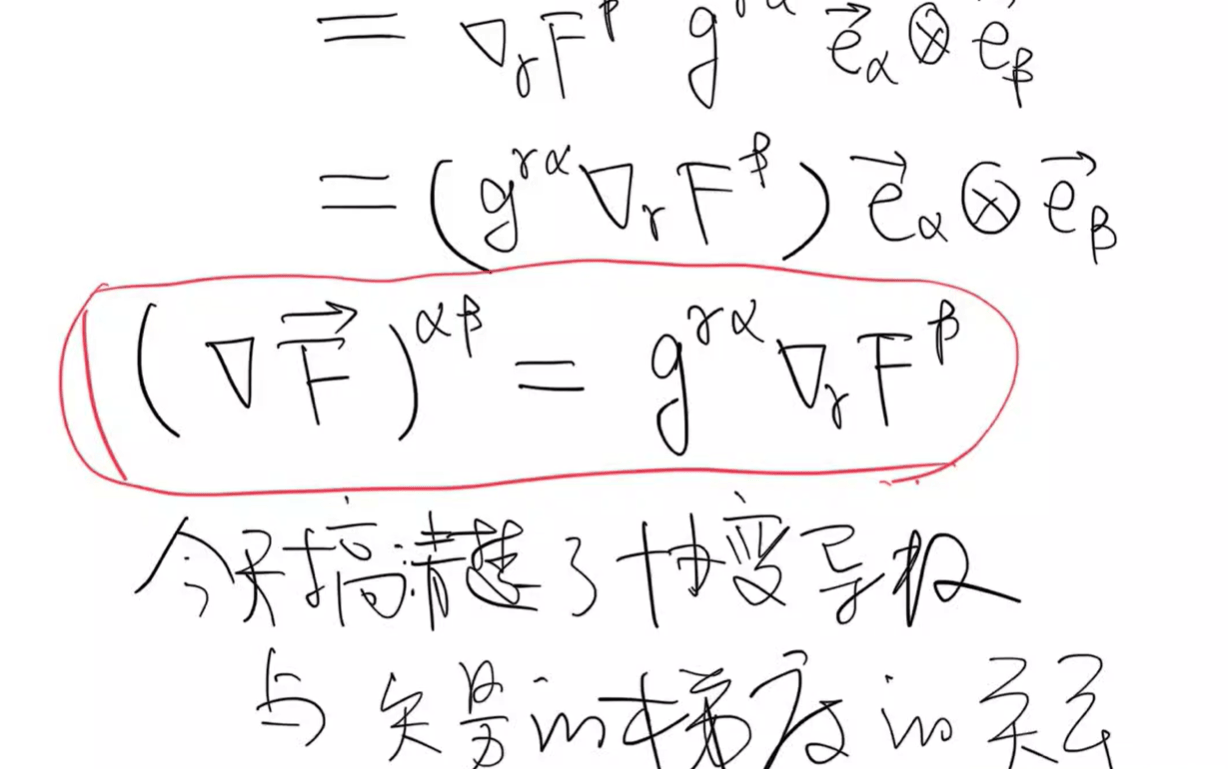 如何从矢量演算变成差异几何变化?男高音的梯度是什么? 5月4日12:00,启动了“张乔阳班级”的245阶段。 Sohu的创始人,董事长兼首席执行官兼物理博士Zhang Chaoyang在Sohu Video Live Broadcast Room中。他首先检查了如何用载体的二元基础语言表达差异的原理,并评估了向上和较低的矢量,男高音和指标的相关含义。接下来,他以向量的双基础语言引入了零级张量(标量)的梯度,本质上是一个一阶男高音,可用于简化任何次要删除下标量场变化的体积的计算。后来,他还比较了这一含义,将梯度引入了一阶张量(向量),并将其与协变量衍生物进行了比较。由向量,力学,电动力学,亲戚,身体定律甚至许多物理量不会改变坐标系统的选择或变化。例如,由于洛伦兹的变化,轻速不会改变。在三维空间中,无论旋转如何,向量的长度保持不变。要了解不变性,通常有必要使用矢量计算工具来描述这些数量或法律。在更一般的情况下,在四维弯曲的时空和一般亲戚相关的空间中对物理定律的研究需要使用更通用的矢量计算,即多样性的几何形状。为什么称为“自定义”几何形状? Pinalzhang Chaoyang说,从差异的角度来看,在几何形状的差异中,人们在歧视中研究了几何特性,并且从其差异的角度来看,从其差异的角度来看,如果时间和空间本身是直的或弯曲的,则可以描述改变空间和空间坐标的物理体积的性质。改变物理带有时空坐标的ICAL数量对应于空间时间坐标的提取的坐标,换句话说是差异。在几何形状的差异中,男高音是重要的事情。当更改坐标系时,张量组件可能会更改,但是张量不会改变。在一般书籍中,经常通过确定在坐标系转换下转换相应的男高音组件的规则来解释男高音的不变性。在PAG研究期间,Zhang Chaoyang发现,与数学的抽象定义相比,基于计算欧几里得空间中向量的经验,使用向量的双基础来理解差异几何变化不仅易于理解,而且在表达计算中也更短。在这类物理学中,他将带领网民审查此方法,然后回答零级张量(标量)和FIR之间的变化的问题T级张量(向量)。这种类型的问题通常在流体机械师等领域遇到,并且我们已经在以前的物理学中与该主题有一些初步联系。张·乔阳首先引入了张量的符号和定义,这与矢量微积分相似,而男高音可以表示为扩展elextextext
他们分别为零,一阶,二阶和三阶男高音。该表示与坐标系无直接相关,这也意味着这些数量不会改变坐标系。选择坐标系后,将获得上下向量,并相应地获得
他们喜欢点产品的关系
一阶张量可以表示为
指数中的f^α称为相反物质。相同的一阶张量也可以表示为
指标在表面的F_α下方是协变量的组件。同样,使用鞋面的不同组合较低的基础向量,二阶男高音可以以不同的形式写入。
张·乔阳提醒人们,上面编写公式的技巧是确保满足爱因斯坦的规则。从这里开始,我们获得了二阶男高音的不同部分,他们的索引写作方法也有所不同。在某些情况下,在上面的公式中描述的,从上到下,(2,0)的物质(或相反物质),(0,2)的物质类型(或协变量成分)和(1,1)张量张量张量张量张量t均受到尊重。对于高阶张量,可以进行类似的讨论和评论。
在介绍了张量的符号和定义之后,我们需要注意特殊的第一阶张量 - 协调惯常的男高音,定义为:
在力学中,它描述了颗粒的小运动,也可以称为切线向量。通过使用点复制,您可以找到坐标的自定义坐标器的长度:
更一般地,可以表示为:
此步骤是指尺度,这是两个基本向量的点的再现
量表的相反也可以通过上层载体的点再现相似地定义
比例尺,反之亦然,能够提起和减少指标。首先,让我们研究如何使用指标来实现基本向量的升力和降低。请注意,基本向量本身也是向量,当量表在基本向量上作用时,
模拟(1),最后一个边缘的均等签名可能被认为是在一组较低的基础向量中扩展的E^β,因此应该有
也就是说,标准将下部基箭头提升到上底箭头。接下来,评估了成分的测量和降低的效果。对于逆变器,有
知道量表可以提高基本向量,因此应该有
也就是说,刻度将逆变器的一部分减少到协变量物质。规模是上层矢量和下基矢量之间的一对一字母。因此,可以认为上层矢量和下基矢量描述了相同的矢量空间,但是选择了两组不同的基本矢量集来研究此空间。
(Zhang Chaoyang介绍了如何使用尺寸指数提升)
零级张量的梯度(标量)
在向量的双重基础的框架中,可以研究不同男高音的梯度的定义。梯度是改变男高音的成本。在三维笔直空间的矩形坐标系中,最多的是零级张量(标量)的总变化。根据多元函数的泰勒的扩展,可以将其写入每个方向的独立变化之和。
同时,在同一坐标系下,坐标的微小变化可以表示为向量
我,j和k是卡特斯中向量的三个方向伊恩坐标。以这种方式,可以以两个向量点的形式重新编写上述变化:
指定向量
这里指定的向量F非常有用。例如,当在去除坐标的某些方向上找到由标量字段引起的变量数时,坐标拆卸方向可能会有所不同,但是找到相应的变量数不需要独立的计算。从上面的派生中,我们可以看到,仅通过了解向量F并通过特定的坐标去除矢量f来产生它,我们就可以得到相应的变化量。张·乔阳(Zhang Chaoyang)介绍了以这种方式指定的向量是梯度,并且不取决于它。对于更改的特定方向,它将是高于原始体积的订单。例如,零阶张量(标量)的梯度这是一阶张量(向量)。
以上仅专注于特殊情况。可以为通用坐标系完成此操作吗? a g零级张量(标量)场是每个坐标的函数。随着泰勒的扩张,一阶男高音可以写为
根据直觉,可以写下以下方程式:
因此,该向量f可以作为
提供了该梯度向量的协变量和相反的组成部分,即扩展下部基矢量和上层载体的系数。同时,可以看出,标量梯度的相对部分可以通过公制升高指数从协变量获得
总之,本节讨论了零级张量梯度的定义。标量的微观变化可以写入不取决于坐标数的微量器和坐标数字微量器的矢量的繁殖点。该向量是梯度,张量遵循的量增加了从标量到向量的顺序。
(张乔阳具有零级t的梯度含义恩索)
一阶张量的梯度(向量)
对于一阶张量(矢量)场,它还可以贝拉兰(Beralan)的变化是由微弹药坐标引起的。类似于零量张量(标量),我们可以定义一阶张量(向量)的梯度,从而简化了发现一阶张量(矢量)更改的问题吗?一阶张量(矢量)的更改是否可以写为二阶张量和坐标微元素?在这个现场班级中,张乔阳还向网民回答了这两个问题。
根据上一节中的想法,有望引入二阶张量t,以表达一阶张量F的变化df的值为
在最后一步中,t扩大(1,1)组件,目的是促进下一次冷凝。继续计算,您可以得到
在括号中是变量值的相对部分
同时,Zhang Chaoyang概括的现场课程解释说樟宜NG应使用协变量衍生物计算一阶张量。这是因为与标量不同,每个张量组件的含义取决于基本向量,它们的更改包括由向量转换引起的组件,这需要仔细处理。使用协变量,
在
γ是与指标兼容的相互作用。将此结果与等式(2)进行比较,可以找到
也就是说,一阶张量的相对部分的协变量是该一阶张量的梯度(二阶张量)的(1,1)部分。
简而言之,一阶张量(矢量)的梯度是二阶张量
物质和基本矢量被指标升高和降低,并且可能会重写:有:
因此,显然我们知道协变量衍生物与矢量梯度之间的关系,实际上它们是同一件事。
(张·乔阳(Zhang Chaoyang)分享了协变量和V之间的关系椭圆梯度)
据了解,周日中午12点在SOHU视频中现场直播“张乔阳班”。网民可以搜索“ Zhang Chaoyang”来“遵循SOHU视频应用程序的流”,以观看实时广播和过去的完整视频重播;关注“张” Chaoyang的物理课程“当然要查看“知识点”的简短视频;此外,您还可以在SOHU新闻应用程序的“ Sohu Technology”帐户上查看每个物理课程的详细文章。
如何从矢量演算变成差异几何变化?男高音的梯度是什么? 5月4日12:00,启动了“张乔阳班级”的245阶段。 Sohu的创始人,董事长兼首席执行官兼物理博士Zhang Chaoyang在Sohu Video Live Broadcast Room中。他首先检查了如何用载体的二元基础语言表达差异的原理,并评估了向上和较低的矢量,男高音和指标的相关含义。接下来,他以向量的双基础语言引入了零级张量(标量)的梯度,本质上是一个一阶男高音,可用于简化任何次要删除下标量场变化的体积的计算。后来,他还比较了这一含义,将梯度引入了一阶张量(向量),并将其与协变量衍生物进行了比较。由向量,力学,电动力学,亲戚,身体定律甚至许多物理量不会改变坐标系统的选择或变化。例如,由于洛伦兹的变化,轻速不会改变。在三维空间中,无论旋转如何,向量的长度保持不变。要了解不变性,通常有必要使用矢量计算工具来描述这些数量或法律。在更一般的情况下,在四维弯曲的时空和一般亲戚相关的空间中对物理定律的研究需要使用更通用的矢量计算,即多样性的几何形状。为什么称为“自定义”几何形状? Pinalzhang Chaoyang说,从差异的角度来看,在几何形状的差异中,人们在歧视中研究了几何特性,并且从其差异的角度来看,从其差异的角度来看,如果时间和空间本身是直的或弯曲的,则可以描述改变空间和空间坐标的物理体积的性质。改变物理带有时空坐标的ICAL数量对应于空间时间坐标的提取的坐标,换句话说是差异。在几何形状的差异中,男高音是重要的事情。当更改坐标系时,张量组件可能会更改,但是张量不会改变。在一般书籍中,经常通过确定在坐标系转换下转换相应的男高音组件的规则来解释男高音的不变性。在PAG研究期间,Zhang Chaoyang发现,与数学的抽象定义相比,基于计算欧几里得空间中向量的经验,使用向量的双基础来理解差异几何变化不仅易于理解,而且在表达计算中也更短。在这类物理学中,他将带领网民审查此方法,然后回答零级张量(标量)和FIR之间的变化的问题T级张量(向量)。这种类型的问题通常在流体机械师等领域遇到,并且我们已经在以前的物理学中与该主题有一些初步联系。张·乔阳首先引入了张量的符号和定义,这与矢量微积分相似,而男高音可以表示为扩展elextextext
他们分别为零,一阶,二阶和三阶男高音。该表示与坐标系无直接相关,这也意味着这些数量不会改变坐标系。选择坐标系后,将获得上下向量,并相应地获得
他们喜欢点产品的关系
一阶张量可以表示为
指数中的f^α称为相反物质。相同的一阶张量也可以表示为
指标在表面的F_α下方是协变量的组件。同样,使用鞋面的不同组合较低的基础向量,二阶男高音可以以不同的形式写入。
张·乔阳提醒人们,上面编写公式的技巧是确保满足爱因斯坦的规则。从这里开始,我们获得了二阶男高音的不同部分,他们的索引写作方法也有所不同。在某些情况下,在上面的公式中描述的,从上到下,(2,0)的物质(或相反物质),(0,2)的物质类型(或协变量成分)和(1,1)张量张量张量张量张量t均受到尊重。对于高阶张量,可以进行类似的讨论和评论。
在介绍了张量的符号和定义之后,我们需要注意特殊的第一阶张量 - 协调惯常的男高音,定义为:
在力学中,它描述了颗粒的小运动,也可以称为切线向量。通过使用点复制,您可以找到坐标的自定义坐标器的长度:
更一般地,可以表示为:
此步骤是指尺度,这是两个基本向量的点的再现
量表的相反也可以通过上层载体的点再现相似地定义
比例尺,反之亦然,能够提起和减少指标。首先,让我们研究如何使用指标来实现基本向量的升力和降低。请注意,基本向量本身也是向量,当量表在基本向量上作用时,
模拟(1),最后一个边缘的均等签名可能被认为是在一组较低的基础向量中扩展的E^β,因此应该有
也就是说,标准将下部基箭头提升到上底箭头。接下来,评估了成分的测量和降低的效果。对于逆变器,有
知道量表可以提高基本向量,因此应该有
也就是说,刻度将逆变器的一部分减少到协变量物质。规模是上层矢量和下基矢量之间的一对一字母。因此,可以认为上层矢量和下基矢量描述了相同的矢量空间,但是选择了两组不同的基本矢量集来研究此空间。
(Zhang Chaoyang介绍了如何使用尺寸指数提升)
零级张量的梯度(标量)
在向量的双重基础的框架中,可以研究不同男高音的梯度的定义。梯度是改变男高音的成本。在三维笔直空间的矩形坐标系中,最多的是零级张量(标量)的总变化。根据多元函数的泰勒的扩展,可以将其写入每个方向的独立变化之和。
同时,在同一坐标系下,坐标的微小变化可以表示为向量
我,j和k是卡特斯中向量的三个方向伊恩坐标。以这种方式,可以以两个向量点的形式重新编写上述变化:
指定向量
这里指定的向量F非常有用。例如,当在去除坐标的某些方向上找到由标量字段引起的变量数时,坐标拆卸方向可能会有所不同,但是找到相应的变量数不需要独立的计算。从上面的派生中,我们可以看到,仅通过了解向量F并通过特定的坐标去除矢量f来产生它,我们就可以得到相应的变化量。张·乔阳(Zhang Chaoyang)介绍了以这种方式指定的向量是梯度,并且不取决于它。对于更改的特定方向,它将是高于原始体积的订单。例如,零阶张量(标量)的梯度这是一阶张量(向量)。
以上仅专注于特殊情况。可以为通用坐标系完成此操作吗? a g零级张量(标量)场是每个坐标的函数。随着泰勒的扩张,一阶男高音可以写为
根据直觉,可以写下以下方程式:
因此,该向量f可以作为
提供了该梯度向量的协变量和相反的组成部分,即扩展下部基矢量和上层载体的系数。同时,可以看出,标量梯度的相对部分可以通过公制升高指数从协变量获得
总之,本节讨论了零级张量梯度的定义。标量的微观变化可以写入不取决于坐标数的微量器和坐标数字微量器的矢量的繁殖点。该向量是梯度,张量遵循的量增加了从标量到向量的顺序。
(张乔阳具有零级t的梯度含义恩索)
一阶张量的梯度(向量)
对于一阶张量(矢量)场,它还可以贝拉兰(Beralan)的变化是由微弹药坐标引起的。类似于零量张量(标量),我们可以定义一阶张量(向量)的梯度,从而简化了发现一阶张量(矢量)更改的问题吗?一阶张量(矢量)的更改是否可以写为二阶张量和坐标微元素?在这个现场班级中,张乔阳还向网民回答了这两个问题。
根据上一节中的想法,有望引入二阶张量t,以表达一阶张量F的变化df的值为
在最后一步中,t扩大(1,1)组件,目的是促进下一次冷凝。继续计算,您可以得到
在括号中是变量值的相对部分
同时,Zhang Chaoyang概括的现场课程解释说樟宜NG应使用协变量衍生物计算一阶张量。这是因为与标量不同,每个张量组件的含义取决于基本向量,它们的更改包括由向量转换引起的组件,这需要仔细处理。使用协变量,
在
γ是与指标兼容的相互作用。将此结果与等式(2)进行比较,可以找到
也就是说,一阶张量的相对部分的协变量是该一阶张量的梯度(二阶张量)的(1,1)部分。
简而言之,一阶张量(矢量)的梯度是二阶张量
物质和基本矢量被指标升高和降低,并且可能会重写:有:
因此,显然我们知道协变量衍生物与矢量梯度之间的关系,实际上它们是同一件事。
(张·乔阳(Zhang Chaoyang)分享了协变量和V之间的关系椭圆梯度)
据了解,周日中午12点在SOHU视频中现场直播“张乔阳班”。网民可以搜索“ Zhang Chaoyang”来“遵循SOHU视频应用程序的流”,以观看实时广播和过去的完整视频重播;关注“张” Chaoyang的物理课程“当然要查看“知识点”的简短视频;此外,您还可以在SOHU新闻应用程序的“ Sohu Technology”帐户上查看每个物理课程的详细文章。








 推荐文章
推荐文章









